这里总结了 LeetCode 上出现的“设计满足要求的数据结构”类题目。
这些题目的解法通常是组合使用常用的数据结构;
只要有了思路,实现并不难,所以本文主要讲解思路。
155. 最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。
我们只需要在原有栈的基础上添加一个数据结构,使其保存当前栈内的最小值即可。因此我们可以使用一个辅助栈,与元素栈同步插入与删除, 实时存储当前元素栈的最小值。
- 当一个元素要入栈时,我们取当前辅助栈的栈顶存储的最小值,与当前元素比较得出最小值,将这个最小值插入辅助栈中;
- 当一个元素要出栈时,我们把辅助栈的栈顶元素也一并弹出;
- 在任意一个时刻,栈内元素的最小值就存储在辅助栈的栈顶元素中。
232. 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty)
将一个栈当作输入栈,用于 push 传入的数据;另一个栈当作输出栈,
用于 pop 和 peek 操作。
push时直接把元素送进输入栈pop或peek时,取输出栈栈顶元素,若输出栈为空则先将输入栈的全部数据依次弹出并压入输出栈,这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序
注意没必要这样做:
push时直接把元素送进输入栈pop或peek时,先将输入栈的全部数据依次弹出并压入输出栈,处理完后将元素再倒腾回输入栈
前者其实与它是等效的,但前者大多数时候,两个栈内都有元素,操作都在栈顶完成,效率高。具体的,时间复杂度:push 和 empty 为 O(1),pop 和 peek 为均摊 O(1)(对于每个元素,至多入栈和出栈各两次,故均摊复杂度为 O(1))。
225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
其实两个队列是多余了,完全可以使用一个队列实现栈的操作。入栈操作时,
首先获得入栈前的元素个数 N,然后将元素入队到队列,再将队列中的前 N 个元素(即除了新入栈的元素之外的全部元素)依次出队并入队到队列,此时队列的前端和后端分别对应栈顶和栈底。
在此基础上出栈操作和获得栈顶元素操作都可以简单实现。
入栈操作时间复杂度为 O(N),其余操作都是 O(1)。
146. LRU 缓存机制
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制 。
实现 LRUCache 类:
LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
LRU 实现方式其实有很多种。
hashmap + 时间戳
把缓存放在 hashmap 中,为新建的每个缓存赋予时间戳(或者版本号、全局时钟值等任何随操作自增的值),在访问时更新时间戳。
淘汰缓存的时机可选在新建缓存时,也可定期进行。
需要淘汰缓存时,遍历整个集合进行 top K 算法淘汰时间戳较小的缓存。
这种算法淘汰缓存时的开销很大。
hashmap + 链表
双向链表按照被使用的顺序存储了这些键值对,靠近头部的键值对是最近使用的,而靠近尾部的键值对是最久未使用的。哈希表则保存缓存数据的键到其在双向链表中的位置(链表结点引用)的映射。
对于 get 操作,首先判断 key 是否存在:
- 如果 key 不存在,则返回 -1;
- 如果 key 存在,则 key 对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置,并将其移动到双向链表的头部,最后返回该节点的值。
对于 put 操作,首先判断 key 是否存在:
- 如果 key 不存在,使用 key 和 value 创建一个新的节点,在双向链表的头部添加该节点,并将 key 和该节点添加进哈希表中。然后判断双向链表的节点数是否超出容量,如果超出容量,则删除双向链表的尾部节点,并删除哈希表中对应的项;
- 如果 key 存在,则与
get操作类似,先通过哈希表定位,再将对应的节点的值更新为 value,并将该节点移到双向链表的头部。
拥有链表结点引用时,拿出该结点仅需拼接前后结点。因此, 在双向链表的实现中,可以使用一个伪头部(dummy head)和一个伪尾部(dummy tail)标记界限, 这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。
访问哈希表的时间复杂度为 O(1),在双向链表的头部添加节点、尾部删除节点的复杂度也为 O(1)。所以 get 与 put 操作的时间复杂度也都为 O(1)。
这个设计看上去很美好,但实际上可能还不如前者。问题在于,“LRU 缓存”中“LRU”仅为淘汰机制,核心还是“缓存”。缓存是干嘛的呢,一来可以作速度匹配(如高速缓存匹配 CPU 与内存的速度),二来能在并行应用间提供共享数据。 考虑一下这个设计的并发性能。因为需要修改链表结构,所以即使是读取不同键的缓存也需要对数据结构整体加锁。反观前面的设计,读写操作几乎可以完全并发。
hashmap + 时间戳 + 随机采样
利用时间戳的设计并发性能好,但是淘汰缓存时遍历整个集合,会带来巨大开销。
为了解决这个瓶颈,可作出牺牲,允许 LRU 近似算法的存在。一种方案是用随机采样代替整体遍历。
具体的,淘汰缓存时只从整个集合中随机选取部分缓存,在这部分缓存中进行 top K 算法淘汰时间戳较小的。不难想到,这种设计在统计意义上与遍历整个集合等效,同时减小了开销。
这种设计在工业项目上有应用,比如 Redis 就是采用了类似的算法。
460. LFU 缓存
请你为 最不经常使用(LFU)缓存算法设计并实现数据结构。
实现 LFUCache 类:
LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象
int get(int key) - 如果键存在于缓存中,则获取键的值,否则返回 -1。
void put(int key, int value) - 如果键已存在,则变更其值;如果键不存在,请插入键值对。当缓存达到其容量时,则应该在插入新项之前,使最不经常使用的项无效。在此问题中,当存在两个或更多个键具有相同使用频率时,应该去除 最近最久未使用 的键。
注意「项的使用次数」就是自插入该项以来对其调用 get 和 put 函数的次数之和。
当一个键首次插入到缓存中时,它的使用次数设置为 1 (由于 put 操作)。
hashmap + 计数器 + 随机采样
仿照上面的 LRU,我们可以把缓存放在 hashmap 中,为新建的每个缓存赋予计数器,
在访问时更新计数器。
淘汰缓存的时机可选在新建缓存时,也可定期进行。
需要淘汰缓存时,随机采样进行 top K 算法淘汰计数器值较小的缓存。
如果坚持要求当存在多个键具有相同使用频次时,去除最久未使用的键,还要额外为每个缓存赋予时间戳。
hashmap + 链表 + 计数器
考虑一下 LRU 的“hashmap + 链表”方案能不能也直接用,即靠近头部的键值对是频次(计数器值)最大的,而靠近尾部的键值对是频次最小的。但是对于 LFU,访问会导致计数器自增,然后这个链表结点不是插入某个特定位置,而是要从当前位置向头部遍历链表,直到更大频次结点或头结点后插入。
最坏情况下遍历耗时 O(N)。
不难想到,耗时增加的原因是相同频次的结点可以有多个。不妨把相同频次的结点打包放在一起,即使用双向链表嵌套,外层链表的结点按频次排序,内层链表放置同频次的缓存,按访问时间排序。
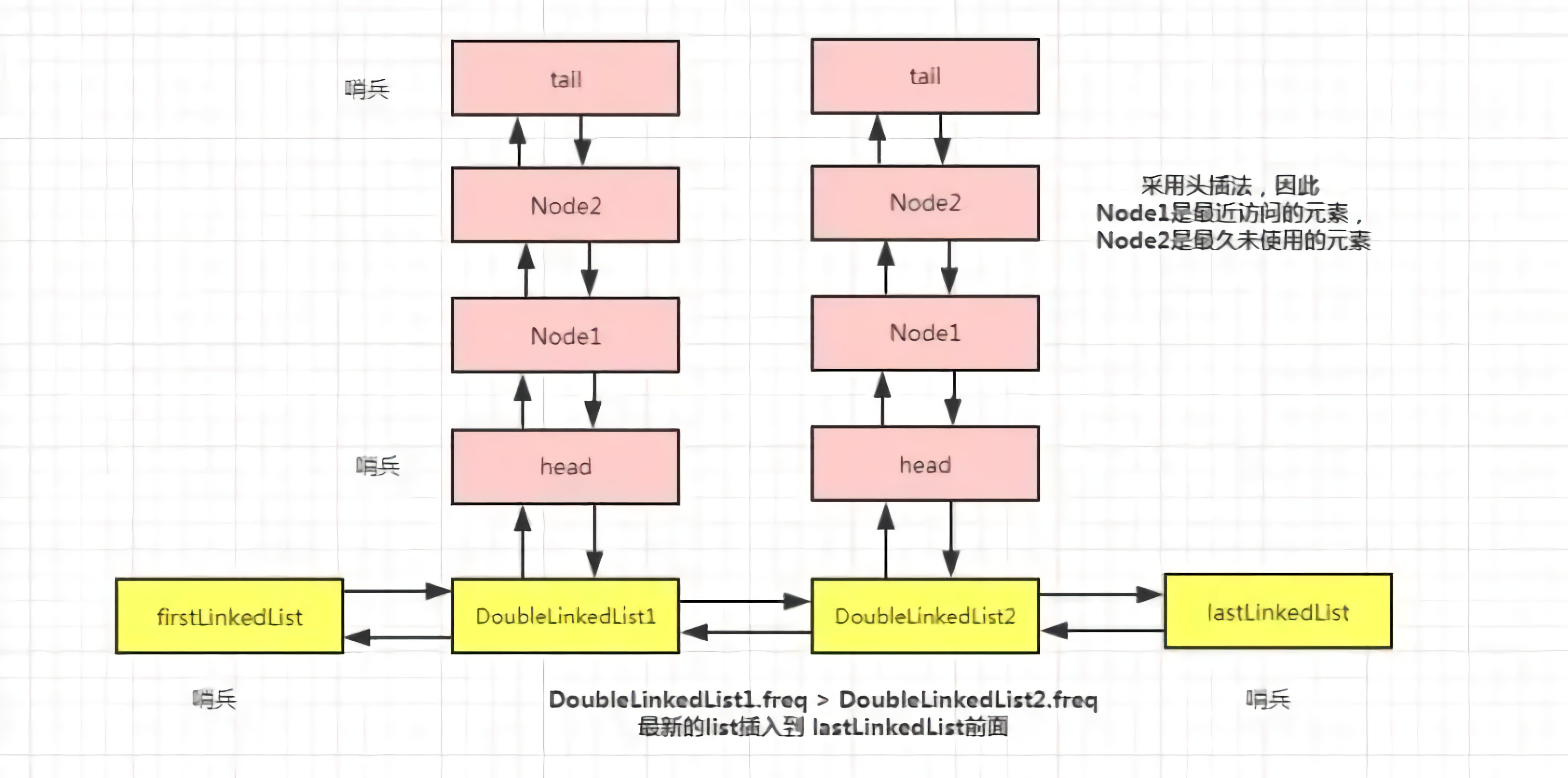
hashmap 记录键到内层链表结点的映射。访问缓存时, 将该结点移动到下一频次对应的内层链表的头部去(如没有,则创建)即可。 淘汰缓存时,先找到外层链表中靠近尾部的结点(频次最小), 再选择其内层链表中靠近尾部的结点(访问时间最久远)。
这种实现效率最高,操作的时间复杂度均为 O(1)。
hashmap + 优先队列
既然每次都淘汰频次最低的,不如用优先队列辅助淘汰,
选择 (计数器值, 时间戳) 元组作为排序的 key。
这种方法在面试等场景下写起来最简单。
题目与部分解答来自力扣(LeetCode)
如果你喜欢我的文章,请我吃根冰棒吧 (o゜▽゜)o ☆

最后附上 GitHub:https://github.com/gonearewe