链表是线性表的一种实现,与数组不同,它通过指针来连接元素。
链表可以在端点以 O(1) 的复杂度删除、插入数据,但随机访问、操作中间的数据的开销是 O(N)。
反转链表
除了最简单的删除、插入外,链表的一大基本操作是反转。
# 反转链表
# 示例:
# 输入: 1->2->3->4->5->NULL
# 输出: 5->4->3->2->1->NULL
// 递归
class Solution {
// 反转链表,返回新的头节点
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode newHead = reverseList(head.next); // 后面已反转链表的头
head.next.next = head; // head.next 指向的结点现在恰好是已反转链表的尾,把当前结点 head 添加到后面去
head.next = null; // 记得清除 head.next
return newHead; // 把已反转链表的头一路传回去
}
}
// 1 -> 2 -> 3 -> 4
//
// after `reverseList(2)`
//
// 1 4 -> 3 -> 2
// | ^
// | |
// -------------
//
// 函数返回的是逆序链表的头结点(4),但是 1 仍然指向 2,由此定位逆序链表的尾结点(2)
# 迭代
class Solution:
def reverseList(self, node: ListNode) -> ListNode:
head, cur = None, node
while cur:
cur.next, cur, head = head, cur.next, cur
return head
# cur 是待处理的原序链表的头结点,head 是已处理的逆序链表的头结点;仅需维护这两个链表
# 5 -> 4 -> 3
# ^
# |
# head
#
# 1 -> 2
# ^
# |
# cur
利用反转可以解决一类问题。例如:
给你两个非空的链表,表示两个非负的整数。它们每个节点存储一位数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例:
输入:
8->2->3->4->NULL
7->5->NULL
输出:
8->3->0->9->NULL
显然,我们分别反转两个链表,即可从低位开始相加(只有这样才能处理进位)。 最后将答案链表再反转一次即可保证形式相同。
我们在后面还将看到更多例子。
双指针
由于链表只进不退的特性,我们经常需要使用双指针来提供额外信息。
快慢指针
例如,如果我们需要得到一个链表的中间结点。可以用两个指针 slow 与 fast 一起遍历链表。slow 一次走一步,
fast 一次走两步。那么当 fast 到达链表的末尾时,slow 必然位于中间。
在此基础上还可以判断一个链表是否为回文链表。可以在找到链表的中点后反转后半部分链表,判断 前半部分链表与后半部分链表的反转是否相等。
快慢指针还经常用于判断链表中是否有环。链表中有环即意味着其中一个结点指向前面的结点,显然,链表中最多只能有一个环。
1 -> 2 -> 3 -> 4
^ |
| _ _ _ _ |
依然有慢指针每次只移动一步,而快指针每次移动两步。如果在移动的过程中,快指针反过来追上慢指针,就说明该链表为环形链表。 否则快指针将先到达链表尾部,该链表不为环形链表。
我们还可以更进一步求出链表开始入环的第一个节点。这要求我们注意“快指针反过来追上慢指针”蕴含的方程关系与“快指针 路程是慢指针两倍”的函数关系。
但是在这之前我们要证明慢指针第一圈走不完一定会和快指针相遇。
首先,快指针先进入环,那么当慢指针刚到达环的入口时,快指针此时在环中的某个位置(也可能此时相遇)。
设此时慢指针到快指针的单向距离为 x(x>=0);设环的周长为 n,那么快指针到慢指针的单向距离为 n-x;
快指针每次都追赶慢指针 1 个单位,设慢指针速度 1/s,快指针 2/s,那么追赶需要 (n-x)s;但在 n-x 秒内,
慢指针只走了 n-x 单位,因为 x>=0,则慢指针走的路程小于等于 n,即走不完一圈就和快指针相遇。
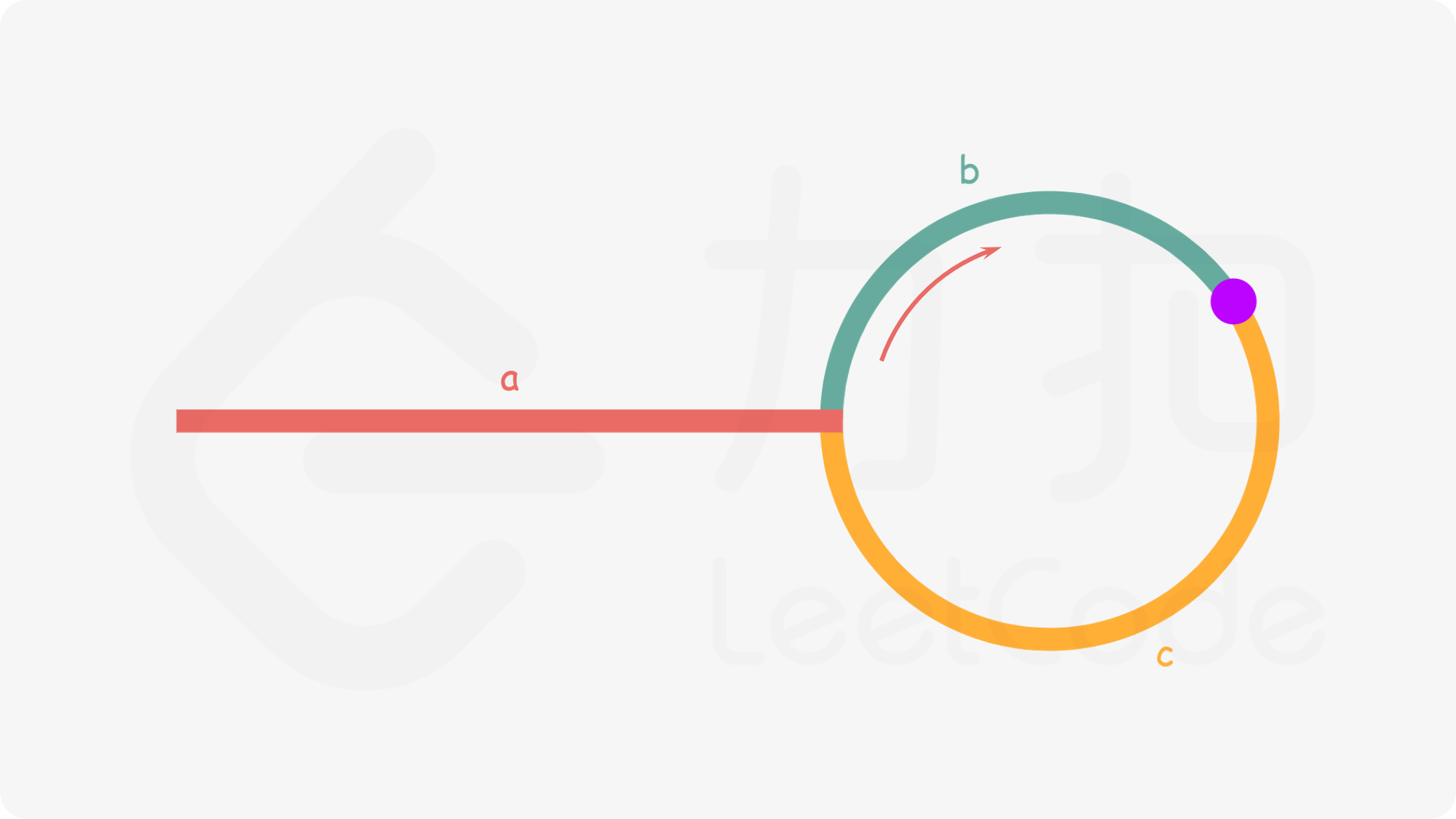
现在设链表中环外部分的长度为 a。slow 指针进入环后,又走了 b 的距离与 fast 相遇。此时,fast 指针已经走完了环的 n 圈,
因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nc。又有它等于慢指针走过的距离 a+b 的两倍。则
a+(n+1)b+nc = 2(a+b) ⟹ a=c+(n−1)(b+c)
我们会发现:从相遇点到入环点的距离加上 n−1 圈的环长,恰好等于从链表头部到入环点的距离。
因此,当发现 slow 与 fast 相遇时,我们再额外使用一个指针 ptr。起始,它指向链表头部;
随后,它和 slow 每次向后移动一个位置。最终,它们会在入环点相遇。
class Solution:
def detectCycle(self, head: ListNode) -> ListNode:
if head is None:
return None
slow = fast = head
while fast.next and fast.next.next:
slow = slow.next
fast = fast.next.next
if fast==slow:
pA,pB = fast,head
while pA != pB:
pA, pB = pA.next, pB.next
return pA
return None
前后指针
前后指针指的是两个指针一前一后,但是速度相等。常用于沿途修改链表的结构。
例如要删除链表的倒数第 N 个结点,我们可以使用两个指针 first 和 second 同时对链表进行遍历,
并且 first 比 second 超前 N 个节点。当 first 遍历到链表的末尾时,second 就恰好处于倒数第 N 个节点。
进阶的问题有 25. K 个一组翻转链表。 需要让“前指针”超前“后指针” K 个单位以进行更新。
# 给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
# k 是一个正整数,它的值小于或等于链表的长度。
# 如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
# 示例 1:
# 输入:head = [1,2,3,4,5], k = 2
# 输出:[2,1,4,3,5]
# 示例 2:
# 输入:head = [1,2,3,4,5], k = 3
# 输出:[3,2,1,4,5]
# 示例 3:
# 输入:head = [1,2,3,4,5], k = 1
# 输出:[1,2,3,4,5]
# 示例 4:
# 输入:head = [1], k = 1
# 输出:[1]
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution:
def reverseKGroup(self, head: ListNode, k: int) -> ListNode:
# 反转链表,返回新的头节点
def reverse(node: ListNode) -> ListNode:
if node is None or node.next is None:
return node
head = reverse(node.next)
node.next.next = node
node.next = None
return head
dummy = ListNode(next=head) # 哨兵结点
# 每个循环开始时,pre,end 指向待反转部分头节点前面的一个节点
pre, end = dummy, dummy
while end:
# 试图跳 k 步
for i in range(k):
end = end.next
if end is None:
break
# end 应指向待反转部分尾部
if end is None:
break
# end 指向再下一个待反转部分头节点,同时清除 end.next 以进行反转
next, end.next = end.next, None
# end 指向的结点现在其实变成了反转链表新的头节点,所以不需要返回值
reverse(pre.next)
# pre.next 指向的结点现在变成反转链表新的尾节点
pre.next.next, pre.next, end = next, end, pre.next
pre = end
return dummy.next # 哨兵结点的 next 其实就是结果的头节点
思考一下,如果是“从尾部开始每 k 个节点一组进行翻转,节点总数不是 k 的整数倍时将头部剩余的节点保持原有顺序”该如何是好; 很简单,先反转链表,然后就变成上面的问题了。
方程关系
我们前面用快慢指针的时候用到了两个指针行程的方程关系,事实上,这样的方程关系也可以单独当成一个主题来谈。
例如,找到两个单链表相交的起始节点。
1 -> 2 -> 3 -> 7 -> NULL
^
|
4 -> 5 -> 6
joint: 3
解法是:
- 指针 pA 指向 A 链表,指针 pB 指向 B 链表,依次往后遍历
- 如果 pA 到了末尾,则令 pA = headB 继续遍历;如果 pB 到了末尾,则 pB = headA 继续遍历
- 若在某一时刻 pA 和 pB 相遇,则到达相交结点(相交结点为 NULL 的话说明事实上不相交)
A 和 B 两个链表长度可能不同,但是 A+B 和 B+A 的长度是相同的,所以遍历 A+B 和遍历 B+A 一定是同时结束。
如果 A,B 相交的话,A 和 B 有一段尾巴是相同的,所以两个遍历的指针一定会同时到达交点;
如果 A,B 不相交的话两个指针就会同时到达 A+B(B+A)的尾节点。
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
pA, pB = headA, headB
while pA != pB:
pA = pA.next if pA else headB
pB = pB.next if pB else headA
return pA
参考:
如果你喜欢我的文章,请我吃根冰棒吧 (o゜▽゜)o ☆

最后附上 GitHub:https://github.com/gonearewe