简介
堆(Heap)是一种特别的完全二叉树。若是满足以下特性,即可称为堆:“给定堆中任意结点 P 和 C,若 P 是 C 的父结点,那么 P 的值会小于等于(或大于等于) C 的值”。若父结点的值恒小于等于子结点的值,此堆称为最小堆(min heap);反之,若父结点的值恒大于等于子结点的值,此堆称为最大堆(max heap)。
复习一下,如果一个深度为 k 的二叉树有 2^(k+1) - 1 个结点,则称为完美二叉树。它的外形是完美无缺的三角形。 而完全二叉树从根结点到倒数第二层满足完美二叉树,最后一层可以不完全填充,其叶子结点都靠左对齐。
由于完全二叉树的良好特性,一般使用线性表存储堆。如下图所示,堆上结点按从上到下、从左到右的顺序存入数组中。
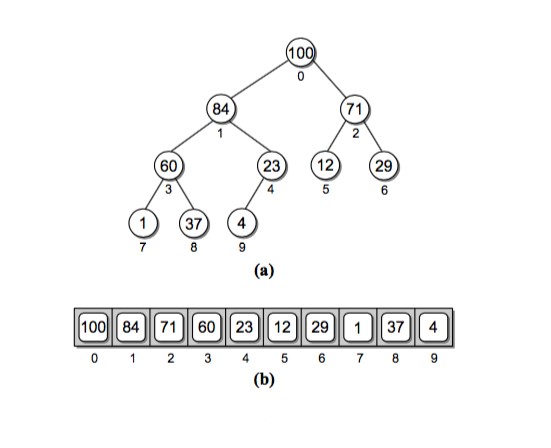
堆支持的操作主要有:push(添加元素)、pop(弹出堆顶)、peek(查看堆顶)。当然,在此过程中始装维持堆特性不变。
实现
下面介绍如何实现堆。
结点索引对应关系
观察数组到堆的下标表示。将数组的索引设为 i。则:
- 左孩子找父结点:
parent(i) = (i - 1) / 2。比如 12 元素的索引为 5,其父亲结点 71 的下标parent(2) = (5 - 1) / 2 = 2; - 右孩子找父结点:
parent(i) = (i - 2) / 2。比如 29 元素找父结点(6 - 2) / 2 = 2;
因为计算机内整数相除会省略小数,所以也可统一为 parent(i) = (i - 1) / 2。
反过来自然得到:
- 父结点找左孩子:
leftChild(i) = parent(i) * 2 + 1。 - 父结点找右孩子:
rightChild(i) = parent(i) * 2 + 2。
上浮与下沉
在此基础上,实现堆要用到两个重要操作:上浮(sift up)与下沉(sift down)。
以最大堆为例。
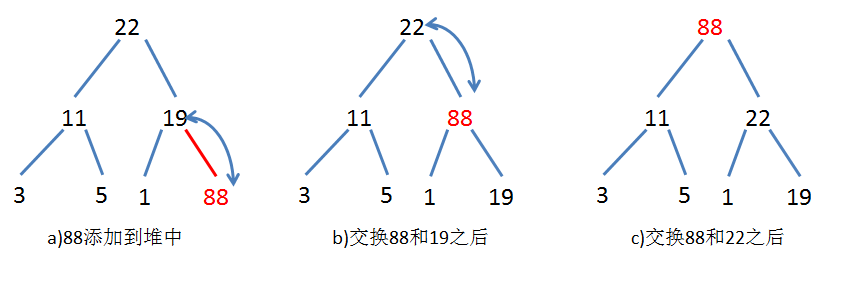
当向堆中添加一个元素时,先将这个元素添加到数组尾。此时一般不满足堆的性质,所以需要将它上浮到合适的位置。 因而将这个新添加的元素和它的父结点进行优先权的比较,如果比父结点的优先权要大,则和父结点交互位置; 然后不断重复和新的父结点比较,直到比新的父结点优先权小或者到达根结点为止。
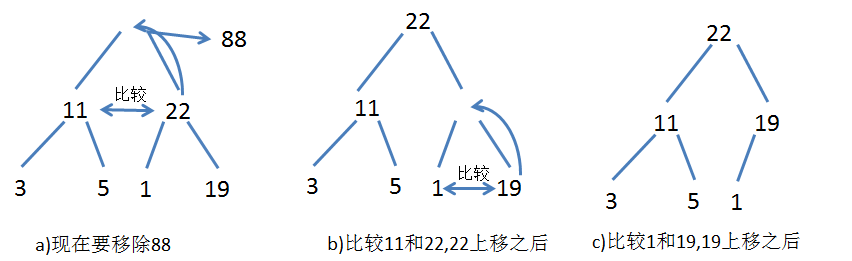
堆只支持弹出根结点。但直接弹出根结点后,堆就会被破坏。此时不妨将数组尾的元素转移到根结点的位置,然后只要让它下沉到合适的位置即可。 注意下沉时元素与左右子结点中的较大值交换。因为只有较大值才能做原来的兄弟结点的根结点,反过来自然不行。
示例
下面实现最小堆,最大堆同理。
class MinHeap:
def __init__(self):
self.li = []
def __len__(self):
return len(self.li)
def _swap(self, i, j):
self.li[i], self.li[j] = self.li[j], self.li[i]
def _sift_up(self, i):
parent = (i - 1) // 2
if parent < 0:
# reached the head
return
if self.li[parent] > self.li[i]:
self._swap(parent, i)
# recursive operation
self._sift_up(parent)
def _sift_down(self, i):
left_child, right_child = i * 2 + 1, i * 2 + 2
if left_child >= len(self) and right_child >= len(self):
# reached the last
return
# must swap with the smaller child
smaller = left_child
if right_child < len(self) and self.li[right_child] < self.li[smaller]:
smaller = right_child
if self.li[smaller] < self.li[i]:
self._swap(smaller, i)
# recursive operation
self._sift_down(smaller)
def push(self, elem):
self.li.append(elem)
self._sift_up(len(self) - 1)
def pop(self):
# swap with the head
self._swap(len(self) - 1, 0)
ret = self.li.pop()
self._sift_down(0)
return ret
def peek(self):
return self.li[0]
应用
堆常用于实现优先队列,而优先队列常用于解决 Top K Element 问题。例如:
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:
你可以假设 k 总是有效的,且 1 ≤ k ≤ 数组的长度。
我们可以维护一个有 K 个元素的最小堆:
- 如果当前堆不满,直接添加;
- 堆满的时候,如果新读到的数小于等于堆顶,肯定不是我们要找的元素,只有新到的数大于堆顶的时候,才将堆顶拿出,然后放入新读到的数。
使用上面实现的最小堆,有:
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
heap = MinHeap()
for i in range(k):
heap.push(nums[i])
for i in range(k, len(nums)):
if nums[i] <= heap.peek():
continue
heap.pop()
heap.push(nums[i])
return heap.peek()
参考:
如果你喜欢我的文章,请我吃根冰棒吧 (o゜▽゜)o ☆

最后附上 GitHub:https://github.com/gonearewe