并查集(Union Find Set)
并查集算法主要用于解决图论中“动态连通性”问题。“连通”即至少可以找到一条从图中一点到另一点的路径, “动态”即图的结点之间的连通关系是一步一步动态增加的。并查集主要需要实现这两个 API:并(合并两个结点, 即连通了两个原本不连通的连通分量,用于动态构建连通关系)与查(判断两个结点是否连通)。
trait UnionFindSet {
def union(p: Int, q: Int): Unit // 将 p 和 q 连接
def connected(p: Int, q: Int): Boolean // 判断 p 和 q 是否连通
}
具体实现时我们使用森林(若干棵树)来构建并查集,而用数组来实现这个森林。 与普通的树不同的是,它的每个结点只有一个指向其父结点的指针;如果它是根结点的话,这个指针指向自己。如果两个结点是连通的,那么它们的根结点是同一个。 那么显然,如果要连通某两个结点,就让其中的任意一个结点的根结点接到另一个结点的根结点上(而不是另一个结点上)。
但是这个朴素的实现时间复杂度不佳。因为树可能会变得非常不平衡,甚至退化成“链表”。
一个简单而有效的方法是路径压缩。只需要对 find 操作(寻找一个结点的根结点的操作)进行一点改动:
递归寻找时,把沿途的所有结点的父结点设为根结点。如下所示:
index 0 1 2 3 4 5 6
parent 1 2 3 3 3 5 6
3 5 6
/ \
4 2
\
1
\
0
图中一共有 3 个连通分量,第一个分量的根结点是 3,它较不平衡。
当执行 find(0) 后,返回根结点 3,同时 0、1 也会都直接指向 3。树高度降低,平衡化。
并查集优化还有其他方法,具体请 Google 搜索或查阅 OI wiki。
路径压缩的并查集 scala 实现如下:
class UnionFindSet(n: Int) {
private val parent = (0 until n).toArray
private def find(a: Int): Int = {
if (parent(a) != a) { // I'm not the root
parent(a) = find(parent(a)) // set my parent to the root
}
parent(a) // return the root
}
def union(a: Int, b: Int): Unit = parent(find(a)) = find(b)
def connected(a: Int, b: Int): Boolean = find(a) == find(b)
}
并查集的两个操作平均时间都仅为 O(α(N)),其中 α(N) 为阿克曼函数(Ackermann)的反函数,其增长极其缓慢,
一般可以认为其单次操作的平均运行时间近似是一个很小的常数。
一些变形包括增加动态记录连通图数目的功能,如题目岛屿数量; 或者是带权并查集,如题目除法求值。 其中动态记录连通图数目可以通过添加单独的字段实现:
private class UnionFindSet {
private final int[] parent;
private int cnt; // 记录连通图数目
UnionFindSet(int n) {
cnt = n;
parent = IntStream.range(0, n).toArray();
}
// 彻底路径压缩(推荐)
int find(int a) {
if (parent[a] != a) { // I'm not the root
parent[a] = find(parent[a]); // set my parent to the root
}
return parent[a]; // return the root
}
void union(int a, int b) {
if (find(a) != find(b)) {
cnt--;
parent[find(a)] = find(b);
}
}
int getCount() {
return cnt;
}
}
最小生成树(Minimum Spanning Tree)
一个连通的生成树是图中的极小连通子图,它包括图中的所有顶点,并且只含尽可能少的边。这意味着对于生成树来说,
若砍去它的一条边,就会使生成树变成非连通图;若给它添加一条边,就会形成图中的一条回路。
对于一个带权连通无向图 G=(V,E),生成树不同,每棵树的权(即树中所有边的权值之和)也可能不同。设 R 是 G 的所有生成树的集合,
若 T 为 R 中边的权值之和最小的那棵生成树,则 T 称为 G 的最小生成树。
最小生成树具有如下性质:
- 最小生成树不是唯一的,即最小生成树的树形不唯一,
R中可能有多个最小生成树。 当图中的各边权值互不相等时,G的最小生成树是唯一的。 - 虽然最小生成树不唯一,但其对应的边的权值之和总是唯一的,而且是最小的。
- 最小生成树的边数为顶点数减一。
- 若无向连通图
G的边比顶点数小 1,即G本身就是一棵树时,G的最小生成树就是它本身。
此外,构造最小生成树的多个算法基本都利用了最小生成树的这个重要性质:
假设
G=(V,E)是一个带权连通无向图,U是顶点集V的一个非空子集。 若(u,v)是满足条件“u含于U,v含于V-U”的边中权值最小的一条, 则必存在一棵包含边(u,v)的最小生成树。
基于该性质的两个常用的最小生成树算法是:Prim 算法和 Kruskal 算法,它们都基于贪心算法, 算法正确性的证明参考《算法导论》。
void prim(G,T){
T=空集; //初始化空树
U={w}; //添加任一顶点w
while((V-U)!=空集){ //若树中不含全部顶点
设(u,v)是满足条件“u 含于 U,v 含于 V-U”的边中权值最小的一条;
T=T并{(u,v)}; //边归入树
U=U并{v}; //顶点归入树
}
}
void Kruskal(V,T){
T=V; //初始化树 T,仅含顶点
numS=n; //不连通分量数
while(numS>1){//如果不连通分量树大于 1
//从 E 中取出权值最小的边(v,u)
if(v 和 u 分别属于 T 中不同的连通分量){
T=T并{(v,u)};//将次边加入生成树
numS--//不连通分量树减1
}
}
}
Prim 算法的实现的具体步骤一般是:
- 新建一个 boolean 数组 visited 用于标记顶点是否已加入 MST,新建一个存储“与 visited 连通子图的边界相邻的顶点”的按“连接边权值”排序的最小堆
- 以图中任意点为起点,以它为 MST 起点,把它的所有相邻顶点(同连接边的权值信息一起)加入最小堆
- 重复下列操作直到最小堆为空:从最小堆中取出边权值最小的顶点,若该点已在 MST 中,进入下一次循环; 否则把这一点加入 MST,把它的所有(不在 MST 内的)相邻点加入最小堆
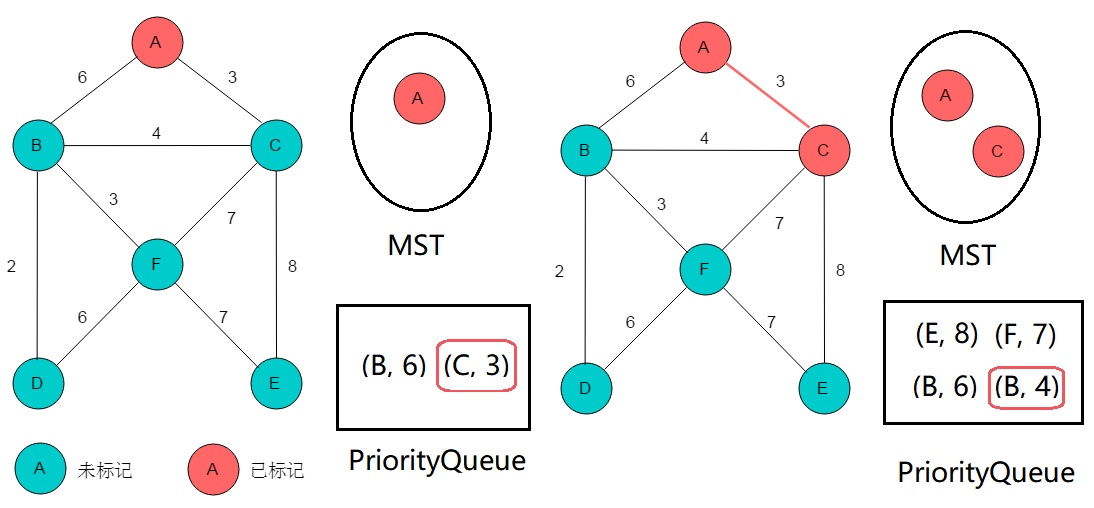
上图中的 PriorityQueue 中的元组表示相邻点 ID 与连接边的权值,其中用红框选中的是下一次循环会被弹出队列的顶点。
在右边的图中,同一顶点 B 存在两个,但是不要紧,权值更小的 (B, 4) 会先被访问,那么 (B, 6) 最终会因为 B 已在 MST 中而被忽略。
具体实现参考后面的 Dijkstra 算法示例,两者有一定的一致性。
而 Kruskal 算法的实现的具体步骤一般是:
- 把所有的边按权值升序排列
- 创建一个空的并查集用于保存 MST 中的点
- 依次遍历每一条边,判断它的两个点是否都已经在并查集里了(即是否在 MST 里): 如是,则跳过;否则,把边记录入 MST,把点加入并查集
Kruskal 算法的练习题有 1489.找到最小生成树里的关键边和伪关键边。
最短路问题
单源最短路问题与 Dijkstra 算法
给定一个带权有向图 G=(V,E),其中每条边的权是一个实数。另外,还给定 V 中的一个顶点,称为源。
要分别计算从源到其他各顶点的最短路径长度。这里的长度就是指路上各边权之和。这个问题通常称为单源最短路径问题。
Dijkstra 算法是一个常用的单源最短路算法,但是它要求每条边的权都是非负实数。它是这样进行的:
- 新建一个 boolean 数组 visited 用于标记顶点到源的最短路是否已最终确定,新建一个存储“与 visited 连通子图的边界相邻的顶点”的按“与源最短路长度”排序的最小堆
- 以源为起点,把它的所有相邻顶点(同更新的“与源最短路长度”一起)加入最小堆
- 重复下列操作直到最小堆为空:从最小堆中取出“与源最短路长度”最小的顶点,若该点已由 visited 标记,进入下一次循环; 否则用 visited 标记这一点,把它的所有(不在 visited 内的)相邻点加入最小堆
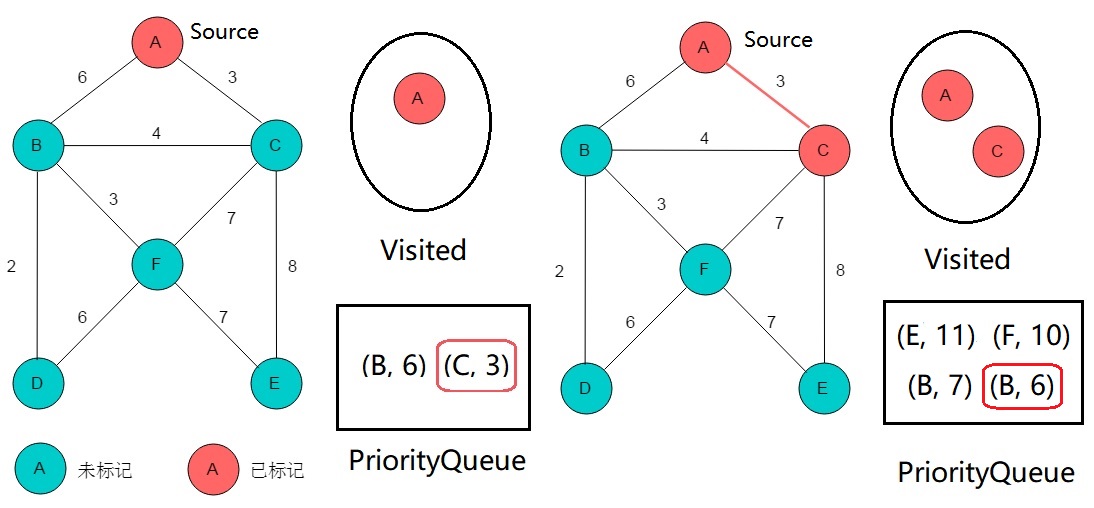
如上图所示,从优先队列中取出 (C, 3) 并用 visited 标记它,即代表顶点 C 对源点 A 的最短路已最终确定为 3。
随后,把相邻点 (B, 3+4),(F, 3+7),(E, 3+8) 加入优先队列以更新它们的最短路信息。
以 743.网络延迟时间 为例介绍具体实现:
// 有 N 个网络节点,标记为 1 到 N。
//
// 给定一个列表 times,表示信号经过有向边的传递时间。 times[i] = (u, v, w),其中 u 是源节点,
// v 是目标节点, w 是一个信号从源节点传递到目标节点的时间。
//
// 现在,我们从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1。
//
// 示例:
// 输入:times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
// 输出:2
//
// 注意:
// N 的范围在 [1, 100] 之间。
// K 的范围在 [1, N] 之间。
// times 的长度在 [1, 6000] 之间。
// 所有的边 times[i] = (u, v, w) 都有 1 <= u, v <= N 且 0 <= w <= 100。
import scala.collection.mutable
import scala.util.control.Breaks.{break, breakable}
object Solution { // Dijkstra
def networkDelayTime(times: Array[Array[Int]], N: Int, K: Int): Int = {
// 初始化 visited
val visited = new Array[Boolean](N + 1)
visited(0) = true
// 使用邻接表存储图
val vertices = new Array[mutable.Set[(Int, Int)]](N + 1)
vertices.indices foreach {
vertices(_) = mutable.Set()
}
times foreach { case Array(src, dst, delay) =>
vertices(src) add(dst, delay)
}
// 优先队列按“与源最短路长度”排序
implicit val ord = Ordering.by[(Int, Int), Int](_._2).reverse
val queue = mutable.PriorityQueue[(Int, Int)]() // (vertex, delaySum)
// Dijkstra 核心代码
var maxDelay = 0
queue.enqueue((K, 0))
while (queue.nonEmpty) {
breakable {
val (cur, delaySum) = queue.dequeue()
if (visited(cur)) break
visited(cur) = true
maxDelay = maxDelay max delaySum // 更新这道题的最终结果
vertices(cur) filterNot { case (vertex, _) => visited(vertex) } foreach {
case (vertex, delay) => queue.enqueue((vertex, delaySum + delay))
}
}
}
if (visited forall identity) maxDelay else -1 // -1 说明图不连通
}
}
多源最短路问题与 Floyd 算法
“多源”顾名思义指的是要求图中任意两点间的最短路长度。解决这个问题的方法 Floyd 算法也十分短小精悍。
简单来说,算法的主要思想是动态规划,核心在于不断地“插点松弛”。
算法的一般步骤为:
- 邻接矩阵 dist 储存当前已知的两点间最短路长度,其最终状态即为我们要的解。初始化时相邻点的最短路为边的权值, 没有直接相连的两点默认为无穷大,而自己与自己的最短路为 0
- 对于每一个顶点,试探经过它的任意两点的最短路会不会因为新加入的点变得更短,如果发生改变,那么两点
(i, j)距离就更新。
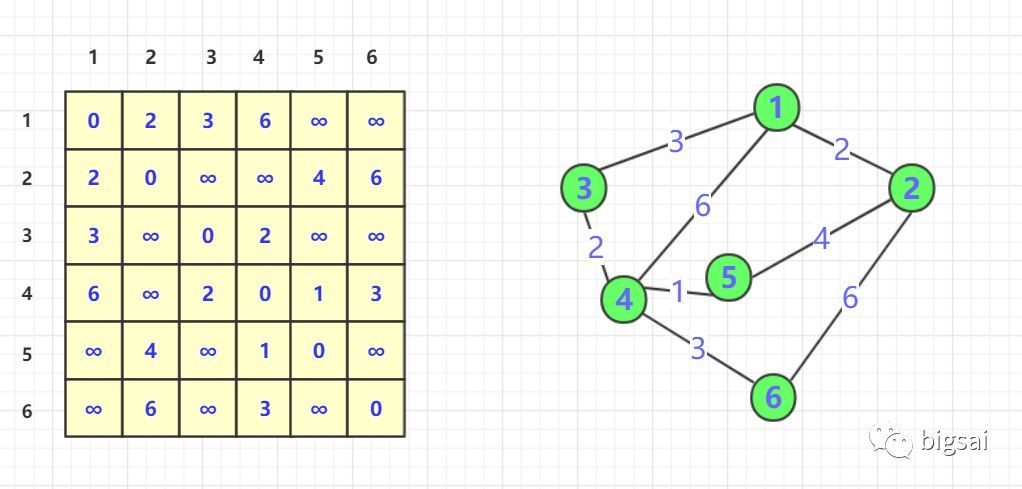
定义状态数组(也就是距离矩阵)dp[k][i][j],表示顶点 i 与顶点 j 通过前 k + 1 个顶点得到的最短距离。
显然,这个最小路径要么不经过第 k 个顶点(由 dp[k-1][i][j] 得到),要么经过(则等于 dp[k-1][i][k] + dp[k-1][k][j]);
归纳得到状态转移方程:
dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k] + dp[k-1][k][j])。
通过状态数组压缩,可以转换为二维 dp。那么自然的,计算时会将 k 放在第一层循环,而将 k 放在最后一层则是常见的错误写法。
具体实现参考 1334.阈值距离内邻居最少的城市 的解答:
// 有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] = [fromi, toi, weighti]
// 代表 fromi 和 toi 两个城市之间的双向加权边,距离阈值是一个整数 distanceThreshold。
//
// 返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。
// 如果有多个这样的城市,则返回编号最大的城市。
//
// 注意,连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。
//
// 示例 1:
// 输入:n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
// 输出:3
// 解释:城市分布图如上。
// 每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是:
// 城市 0 -> [城市 1, 城市 2]
// 城市 1 -> [城市 0, 城市 2, 城市 3]
// 城市 2 -> [城市 0, 城市 1, 城市 3]
// 城市 3 -> [城市 1, 城市 2]
// 城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市,但是我们必须返回城市 3,因为它的编号最大。
//
// 示例 2:
// 输入:n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
// 输出:0
// 解释:城市分布图如上。
// 每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是:
// 城市 0 -> [城市 1]
// 城市 1 -> [城市 0, 城市 4]
// 城市 2 -> [城市 3, 城市 4]
// 城市 3 -> [城市 2, 城市 4]
// 城市 4 -> [城市 1, 城市 2, 城市 3]
// 城市 0 在阈值距离 4 以内只有 1 个邻居城市。
//
// 提示:
// 2 <= n <= 100
// 1 <= edges.length <= n * (n - 1) / 2
// edges[i].length == 3
// 0 <= fromi < toi < n
// 1 <= weighti, distanceThreshold <= 10^4
// 所有 (fromi, toi) 都是不同的。
object Solution {
def findTheCity(n: Int, edges: Array[Array[Int]], distanceThreshold: Int): Int = {
val dp = new Array[Array[Int]](n)
dp.indices foreach {
dp(_) = new Array[Int](n)
}
dp.indices foreach { i =>
dp(i).indices foreach { j =>
dp(i)(j) = Int.MaxValue
}
}
edges foreach { case Array(v1, v2, weight) =>
dp(v1)(v2) = weight
dp(v2)(v1) = weight
}
// Floyd Algorithm 核心代码
for {
k <- 0 until n // 注意 k 必须在最外层
i <- 0 until n
j <- 0 until n
if i != j && dp(i)(k) != Int.MaxValue && dp(k)(j) != Int.MaxValue
} {
dp(i)(j) = dp(i)(j) min dp(i)(k) + dp(k)(j)
}
// 计算结果
dp.indices map { i => i -> dp(i).count(w => w <= distanceThreshold) } reduceLeft {
(min, cur) =>
min match {
case (id, w) => if (cur._2 <= w) cur else min
}
} match {
case (id, _) => id
}
}
}
拓扑排序(Topological sorting)与 Kahn 算法
拓扑排序要解决的问题是给一个图的所有节点排序。
在一个 DAG(Directed Acyclic Graph,有向无环图)中,我们将图中的顶点以线性方式进行排序,使得对于任何的顶点 u 到 v 的有向边 (u, v),都有 u 在 v 的前面。
拓扑排序的目标也可描述为将所有节点排序,使得排在前面的节点不能依赖于排在后面的节点。
实现思路很简单:初始状态下,集合 S 装着所有入度为 0 的点,L 是一个空列表;
每次从 S 中取出一个点 u(可以随便取)放入 L,然后将 u 的所有边 (u, v1),(u, v2),(u, v3)… 删除,对于边 (u, v),若将该边删除后点 v 的入度变为 0,则将 v 放入 S 中;
不断重复以上过程,直到集合 S 为空;检查图中是否存在任何边,如果有,那么这个图一定有环路,否则正常结束且 L 中顶点的顺序就是拓扑排序的结果。
参考实现:
vector<int> G[MAXN]; // vector 实现的邻接表
int c[MAXN]; // 标志数组
vector<int> topo; // 拓扑排序后的节点
bool dfs(int u) {
c[u] = -1;
for (int v : G[u]) {
if (c[v] < 0)
return false;
else if (!c[v])
if (!dfs(v)) return false;
}
c[u] = 1;
topo.push_back(u);
return true;
}
bool toposort() {
topo.clear();
memset(c, 0, sizeof(c));
for (int u = 0; u < n; u++)
if (!c[u])
if (!dfs(u)) return false;
reverse(topo.begin(), topo.end());
return true;
}
时间复杂度 O(E+V),空间复杂度 O(V)。
拓扑排序可以用来判断图中是否有环,还可以用来判断图是否是一条链。
参考:
最后附上 GitHub:https://github.com/gonearewe