马拉车算法(Manacher’s Algorithm)用于在 O(N) 时间内提取一个字符串中有关回文串的信息。
“回文串”是一个正读和反读都一样的字符串,比如“level”或者“noon”等等就是回文串, 单个字符,重复的字符同样是回文串。鉴于它的中心对称性,不难想到判断一个字符串是回文串的 方法是在循环内依次判断对称位置的字符是否相同。但是如果要找出一个字符串中的最长回文串, 或者计数存在的所有回文串,我们就需要在外层再枚举每一个子串,时间复杂度较高。 而马拉车算法充分利用回文串的对称性以简化计算。
以下转载自windliang 的知乎文章《一文让你彻底明白马拉车算法》
插入占位符
首先我们需要解决下奇数和偶数的问题,在原字符串中插入未出现的字符作占位符。例如,在每个字符间插入”#”, 并且为了使得扩展的过程中,到边界后自动结束,在两端分别插入 “^” 和 “$”,这样中心扩展的时候, 判断两端字符是否相等的时候,如果到了边界就一定会不相等,从而出了循环。经过处理,字符串的长度永远都是奇数了, 后面进行中心扩展时情况就简化了。
a -> ^#a#$
aa -> ^#a#a#$
abc -> ^#a#b#c#$
设原字符串长度 n,插入 # 后长度为 n + n + 1,插入起始字符后长度为 2n + 3,必为奇数。
回文串长度
首先我们用一个数组 P 保存从中心扩展的回文串的最大半径,而它刚好也是去掉 “#” 的原回文串的总长度。
例如下图中下标是 6 的地方。可以看到 P[6] 等于 5,所以它是向左边扩展 5 个字符,相应的右边也是扩展 5 个字符,
也就是 “#c#b#c#b#c#”。而去掉 # 恢复到原来的字符串,变成 “cbcbc”,它的长度刚好也就是 5。
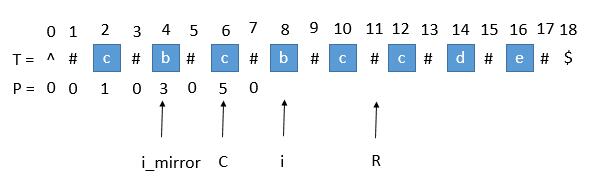
回文串位置
用 P 的下标 i 减去 P[i],再除以 2 ,就是原回文串的开头下标了。
例如在上图中,我们找到 P[i] 的最大值为 5 ,也就是回文串的最大长度是 5 ,对应的下标是 6 ,
所以原字符串的开头下标是 (6 - 5) / 2 = 0。
求 P[i]
接下来是算法的关键了,它充分利用了回文串的对称性。
我们用 C 表示回文串的中心,用 R 表示回文串的右边半径(包含)对应的下标。所以有 R = C + P[i]。
C 和 R 所确定的回文串是当前循环中 R 最靠右的回文串。
让我们考虑求 P[i] 的时候,如下图。
用 i_mirror 表示当前需要求的第 i 个字符关于 C 对称的下标。

我们现在要求 P[i],如果是用中心扩展法,那就向两边扩展比对就行了。但是我们其实可以利用回文串 C 的对称性。
i 关于 C 的对称点是 i_mirror,P[i_mirror] = 3,所以 P[i] 也等于 3 。
但是有三种情况将会造成直接赋值为 P[i_mirror] 是不正确的,下边一一讨论。
1)超出了 R

当我们要求 P[i] 的时候,P[mirror] = 7,而此时 P[i] 并不等于 7 。为什么呢,因为我们从 i 开始往后数 7 个,
等于 22 ,已经超过了最右的 R 。此时不能利用对称性了,但我们一定可以扩展到 R 的,所以 P[i] 至少等于 R - i = 20 - 15 = 5。
会不会更大呢,我们只需要比较 T[R+1] 和 T[R+1] 关于 i 的对称点就行了,就像中心扩展法一样一个个扩展。
2)P[i_mirror] 遇到了原字符串的左边界
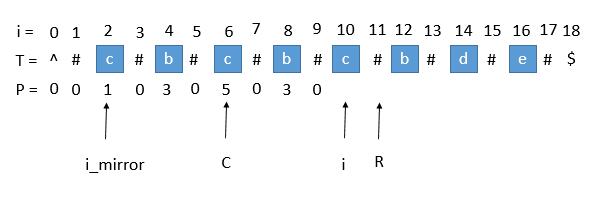
此时 P[i_mirror] = 1,但是 P[i] 赋值成 1 是不正确的。出现这种情况的原因是 P[i_mirror] 在扩展的时候首先是 "#" == "#",
之后遇到了 “^” 和另一个字符比较,也就是到了边界,才终止循环的。而 P[i] 并没有遇到边界,
所以我们可以继续通过中心扩展法一步一步向两边扩展就行了。
3)i 等于了 R
此时我们先把 P[i] 赋值为 0 ,然后通过中心扩展法一步一步扩展就行了。
C 和 R 的更新
就这样一步一步的求出每个 P[i],当求出的 P[i] 的右边界大于当前的 R 时,我们就需要更新 C 和 R 为当前的回文串了。
因为我们必须保证 i 在 R 里面,所以一旦有更右边的 R 就要更新 R。
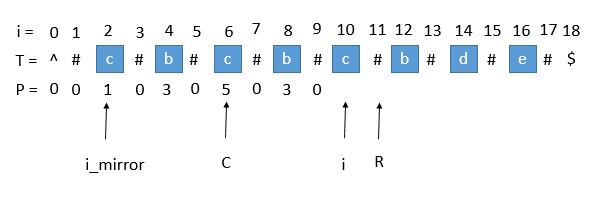
此时的 P[i] 求出来将会是 3 ,P[i] 对应的右边界将是 10 + 3 = 13。所以大于当前的 R ,我们需要把 C 更新成 i 的值,
也就是 10 ,R 更新成 13。继续下边的循环。
代码模板
private String preprocess(String s) {
if (s.length() == 0) {
return "^$";
}
var str = new StringBuilder(s.length() * 2 + 3);
str.append("^"); // prefix
for (var c : s.toCharArray()) {
str.append("#");
str.append(c);
}
str.append("#$");
return str.toString();
}
public xxx palindrome(String s) {
String T = preprocess(s);
int[] P = new int[T.length()];
int C = 0, R = 0; // init
// 马拉车核心代码
for (int i = 1; i < T.length() - 1; i++) { // i 为 0、T.length()-1 对应前缀,后缀,P[i] 必为 0
int i_mirror = 2 * C - i;
// 简洁版这么写
// P[i] = R > i ? Math.min(R - i, P[i_mirror]) : 0;
if (R > i) {
P[i] = Math.min(R - i, P[i_mirror]); // 防止超出 R
} else { // R == i 或者循环开始时 R < i
P[i] = 0;
}
// 碰到之前讲的三种情况时候,需要利用中心扩展法
while (T.charAt(i + 1 + P[i]) == T.charAt(i - 1 - P[i])) {
P[i]++;
}
// 判断是否需要更新 R
if (i + P[i] > R) {
C = i;
R = i + P[i];
}
}
// 1. 求最长回文子串
int maxLen = 0;
int centerIndex = 0;
for (int i = 1; i < n - 1; i++) { // 找出 P 的最大值
if (P[i] > maxLen) {
maxLen = P[i];
centerIndex = i;
}
}
int start = (centerIndex - maxLen) / 2; // 最开始讲的求原字符串下标
return s.substring(start, start + maxLen);
// 2. 求回文子串数目
// 设 a = P[i],其代表 i 对应的最长回文串的长度,
// 而长为 a 的回文串又共计包含 (a + 1) / 2 个回文子串,
// 比如长为 5 的回文串包含长为 5,3,1 的回文子串,
// 长为 4 的回文串包含长为 4,2 的回文子串。
return Arrays.stream(P).map(a -> (a + 1) / 2).sum();
}
回文串的其他算法与性质
马拉车算法是专门用于解决回文串问题的算法,但不是每个回文串的问题用马拉车算法解决都简单。 比如,可以使用动态规划找出字符串中的回文子串。
class Solution {
// 最长回文子串
public String longestPalindrome(String s) {
int n = s.length();
boolean[][] dp = new boolean[n][n];
String ans = "";
// 考虑状态转移公式,并以此确定扫描方向
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
if (j == i) {
dp[i][j] = true;
} else if (j == i + 1) {
dp[i][j] = (s.charAt(j) == s.charAt(i));
} else {
dp[i][j] = ((s.charAt(j) == s.charAt(i)) && dp[i + 1][j - 1]);
}
if (dp[i][j] && (j - i + 1 > ans.length())) {
ans = s.substring(i, j + 1);
}
}
}
// 不仅仅可以用来找最长回文子串,事实上 dp 数组内存储着所有的回文子串
return ans;
}
}
再考虑一下这个问题:
131. 分割回文串
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: "aab"
输出:
[
["aa","b"],
["a","a","b"]
]
通过 DFS 搜索求解是最直观、最简单的思路。而使用动态规划寻找所有回文串的预处理可以把
判断枚举到的字符串是不是回文串的操作变成 O(1) 操作。思考一下使用马拉车算法作预处理要怎么写,以及可不可以
不进行字符串的 DFS 搜索,直接在马拉车的结果基础上进行搜索。
有的问题就完全用不到马拉车算法了。一般回文串问题经常与区间动态规划、双指针等有关。 考虑动态规划问题 516.最长回文子序列:
给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度。可以假设 s 的最大长度为 1000 。
示例 1:
输入:
"bbbab"
输出:
4
一个可能的最长回文子序列为 "bbbb"。
示例 2:
输入:
"cbbd"
输出:
2
一个可能的最长回文子序列为 "bb"。
提示:
1 <= s.length <= 1000
s 只包含小写英文字母
设 dp[i][j] 表示 s 的第 i 个字符到第 j 个字符组成的子串中,最长的回文序列的长度,思考状态转换公式是什么。
另外推荐 LeetCode 上的回文串练习, 尤其推荐这几题:
前两题利用了从回文串对称性延伸的性质:
假设存在两个字符串 s1 和 s2,s1 可与 s2 拼接成一个回文串,则必有:
- 若
s1和s2长度相等,则s1.reverse == s2; - 若
s1和s2长度不等,且设s1是较长串,s1 = t1 + t2,则有t1是回文串而t2.reverse == s2(此时s2 + s1是回文串)或者t2是回文串而t1.reverse == s2(此时s1 + s2是回文串)
最后两题涉及了回文串的枚举方法:枚举“回文根”作对称(所有自然数都可作为回文根)。比如:回文根“123”对应“123321”和“12321”;回文根“1”对应“1”和“11”;特别的,回文根“0”只对应“0”本身,因为“00”不是数字的合法表示形式。
最后附上 GitHub:https://github.com/gonearewe