写在前面
二叉树是一种基本的数据结构,学好它对于深刻理解递归、二分法以及后续学习图帮助很大; 而且,树形结构也是开发中经常用到的结构。对于二叉树来说,最基本的操作就是遍历, 通过遍历每一个结点,有时候就可以解决很多的问题。遍历分为两种:广度优先搜索(BFS) 和深度优先搜索(DFS)。其中广度优先搜索一般利用队列以迭代法进行,一般又叫做层次遍历, 顾名思义,它是从根结点一层一层向下遍历;深度优先搜索既可以以形式简单的迭代法进行,又可以 通过利用栈以迭代法进行,对于迭代法,我们先介绍教科书上教的一般方法,再介绍转载的 博客上的更加简单的方法。
广度优先搜索(层次遍历)
如果我们直接访问左孩子,毫无疑问就会因为无法返回父结点而丢掉右孩子。所以, 我们需要沿途保存路径信息。我们要确保某一层全部遍历完了才去访问下一层,所以 应该是 FIFO 的需求,因此我们使用队列。每次我们从队列中取出一个结点,处理它, 然后把它的左右孩子(如果有的话)放进队列。队列中保存着未处理的结点,只要队列 不为空,重复以上操作。当然,初始时我们要把非空的根结点放进队列以开始循环。
public ArrayList<Integer> levelOrderTraverse(){
var cur=this;
var queue=new LinkedList<BinaryTree>();
var result=new ArrayList<Integer>();
if (cur==null){ // 判断空树
return result;
}
queue.offer(cur); // 根结点初始入队
while(!queue.isEmpty()){ // 只要队列非空,取出一个结点并处理,然后把其左右孩子入队
cur =queue.poll();
result.add(cur.value); // 处理当前结点
// 左右孩子入队
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
return result;
}
BFS 的优势在于可以方便地知道二叉树的高度(或者叫深度)信息以及可以分层处理结点(统计 二叉树每层结点个数,计算每层结点平均值等)。但是,在上面的写法中,每一个外循环(其实 只有一个循环)处理一个结点,不容易知道当前结点的信息。所以,我们通常写出下面的形式。
public int minDepth(TreeNode root) { // 这是一个计算二叉树最小深度的程序
if (root == null) {
return 0;
}
var depth = 1;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root); // 根结点初始入队
while (!queue.isEmpty()) {
var len = queue.size(); // 计算当前层结点数
for (int i = 0; i < len; i++) { // 依次处理当前层所有的结点
var cur = queue.poll();
if (cur.left == null && cur.right == null) {
return depth; // 发现叶子结点,立刻返回深度
}
// 左右孩子入队
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
depth++; // 搜索完每一层都要更新深度
}
return depth; // 其实永远都不会运行到这
}
我们在进入每一个内循环前记录下队列的长度,这就是当前层的结点数。内循环每次只 处理一层的结点,外循环每次下降一层。它们一个记录横向的位置,另一个记录纵向的位置, 我们很容易就可以知道结点的状态信息。所以,下一次碰到有关二叉树高度或者处理每一层的 问题时,你就要考虑 BFS 了。
深度优先搜索的递归法
深度优先搜索按根结点处理的顺序分为先序遍历(preorder traversal)、中序遍历 (inorder traversal)、后序遍历(postorder traversal)。先序、中序、后序 处理(process)(注意不是访问(visit),本文中“访问”指程序看到了此结点,“处理”指对结点 保存的值进行具体的操作)结点的顺序分别是“根-左-右”、“左-根-右” 和 “左-右-根”; 也就是说,所谓先序就是先处理根结点,以此类推;而且可以发现,左孩子结点永远比 右孩子结点先处理,这是约定俗成的顺序,先左还是先右只会影响遍历顺序,如果你 要做的事依赖于顺序,你可以根据实际情况选择先左先右。
递归法写起来是很简单的,三种顺序的形式也比较统一。
// 先序遍历
void preorder(TreeNode *root, vector<int> &path)
{
if(root != NULL)
{
path.push_back(root->val);
preorder(root->left, path);
preorder(root->right, path);
}
}
// 中序遍历
void inorder(TreeNode *root, vector<int> &path)
{
if(root != NULL)
{
inorder(root->left, path);
path.push_back(root->val);
inorder(root->right, path);
}
}
// 后序遍历
void postorder(TreeNode *root, vector<int> &path)
{
if(root != NULL)
{
postorder(root->left, path);
postorder(root->right, path);
path.push_back(root->val);
}
}
可以看到只是处理结点(放进 vector)的顺序不同。当然,我们一般是这样写递归函数的
void preorder(TreeNode *root, vector<int> &path)
{
if(root == NULL) return;
path.push_back(root->val);
preorder(root->left, path);
preorder(root->right, path);
}
我们把递归结束的条件放在一开始,递归每一步的处理放在后面。不难发现这两种写法是等价的。
递归形式适合解决递归类问题(这不是废话吗)。比如,求二叉树的最大深度时, 由二叉树的底部到当前结点的深度等于左右子树的深度中的较大值加一(当前结点高一个单位), 递归的结束条件是空结点的高为零。
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
// var leftDepth = maxDepth(root.left);
// var rightDepth = maxDepth(root.right);
// return 1+ Math.max(leftdepth + rightDepth);
// 简写为以下形式
return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
}
注意这里求解的 maxDepth 可以通过递归计算子树的 maxDepth 来获得,但是对于更复杂的问题, 递归函数应定义成可以传递状态的,而最终结果通过全局变量更新。例如 124. 二叉树中的最大路径和:
# 路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中至多出现一次。
# 该路径至少包含一个节点,且不一定经过根节点。
# 路径和 是路径中各节点值的总和。
# 给你一个二叉树的根节点 root ,返回其最大路径和。
# 示例 1:
# 1
# / \
# 2 3
# 输入:root = [1,2,3]
# 输出:6
# 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
# 示例 2:
# -10
# / \
# 9 20
# / \
# 15 7
# 输入:root = [-10,9,20,null,null,15,7]
# 输出:42
# 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
# 提示:
# 树中节点数目范围是 [1, 3 * 104]
# -1000 <= Node.val <= 1000
class Solution:
def maxPathSum(self, root: TreeNode) -> int:
self.ans = -10 ** 10
# self 定义成员变量,以保证内部函数可以修改 ans
# dfs 计算以 node 为起点向下延伸的一条路径,该路径上的节点值之和最大。
def dfs(node: TreeNode) -> int:
if not node:
return 0
l_max = max(0, dfs(node.left))
r_max = max(0, dfs(node.right))
self.ans = max(self.ans, node.val + l_max + r_max)
# 以 node 为根的最大路径和
return node.val + max(l_max, r_max) # dfs 的返回值必须加上 node.val,因为它是起点
dfs(root)
return self.ans
推荐练习题目:
深度优先搜索的迭代法
递归的效率一般不佳,所以也需要迭代写法。要想迭代,我们就必须手动维护一个 堆栈以弥补函数调用栈的缺失。教科书上一般这样写
# 非递归先序遍历
def preorderTraversal(self, root: TreeNode):
stack = []
p = root
while stack or p:
while p:
stack.append(p)
process(p)
p = p.left
if stack:
p = stack.pop()
p = p.right
# 非递归中序遍历
def inorderTraversal(self, root: TreeNode):
stack = []
p = root
while stack or p:
while p:
stack.append(p)
p = p.left
if stack:
p = stack.pop()
process(p)
p = p.right
# 非递归后序遍历
def postorderTraversal(self, root: TreeNode):
stack = []
p = root
last = None
while stack or p:
while p:
stack.append(p)
p = p.left
if stack:
p = stack.pop()
if p.right is None or p.right == last:
process(p)
last = p
p = None
continue
stack.append(p)
p = p.right
我们使用栈沿途保存路径。每一次外循环开始时,我们不断把当前结点入栈保存直到碰到叶子结点。 然后从栈中取结点并切换到它的右子树。先序与中序的区别在于处理结点的时机。也就是说, 我们一路向左走到头,看一下堆栈,堆栈不为空说明有回头路可走,回头转向右子树,然后 循环往复,再一路向左走到头……直到某一次走到头时发现没有回头路了,说明所有结点都处理完了,程序 完成。
但是可以发现,后序遍历的实现的复杂程度明显高于先序遍历和中序遍历。因为后序遍历
要求最后处理根结点,所以切换到右子树前必须把根结点再放回堆栈。那么问题来了,
根结点会在堆栈中出现两次,我要怎样才可以知道现在是第几次访问当前结点,所以我们
使用了额外的东西来保存这一信息。通过 p.right == last 我们可以获悉上一个处理的结点是不是右孩子,即是不是轮到处理自己了。
而且先序遍历和中序遍历看似实现风格一样,但是实际上前者是在指针迭代时处理结点值, 后者是在栈顶处理结点值,实现思路还是有一点不统一的。
深度优先搜索的迭代法改良版
以下内容部分来自别人的博客,链接见文章最后。
// 更简单的非递归先序遍历
void preorderTraversalNew(TreeNode *root, vector<int> &path)
{
stack< pair<TreeNode *, bool> > s;
s.push(make_pair(root, false));
bool visited;
while(!s.empty())
{
root = s.top().first;
visited = s.top().second;
s.pop();
if(root == NULL)
continue;
if(visited)
{
path.push_back(root->val);
}
else
{
s.push(make_pair(root->right, false));
s.push(make_pair(root->left, false));
s.push(make_pair(root, true));
}
}
}
// 更简单的非递归中序遍历
void inorderTraversalNew(TreeNode *root, vector<int> &path)
{
stack< pair<TreeNode *, bool> > s;
s.push(make_pair(root, false));
bool visited;
while(!s.empty())
{
root = s.top().first;
visited = s.top().second;
s.pop();
if(root == NULL)
continue;
if(visited)
{
path.push_back(root->val);
}
else
{
s.push(make_pair(root->right, false));
s.push(make_pair(root, true));
s.push(make_pair(root->left, false));
}
}
}
// 更简单的非递归后序遍历
void postorderTraversalNew(TreeNode *root, vector<int> &path)
{
stack< pair<TreeNode *, bool> > s;
s.push(make_pair(root, false));
bool visited;
while(!s.empty())
{
root = s.top().first;
visited = s.top().second;
s.pop();
if(root == NULL)
continue;
if(visited)
{
path.push_back(root->val);
}
else
{
s.push(make_pair(root, true));
s.push(make_pair(root->right, false));
s.push(make_pair(root->left, false));
}
}
}
以上三种遍历实现代码行数一模一样,如同递归遍历一样,只有三行核心代码的先后顺序有区别。 为什么能产生这样的效果?
有重合元素的局部有序一定能导致整体有序
这就是我得以统一三种更简单的非递归遍历方法的基本思想, 如下第一段序列,局部 2 3 4 和局部 1 2 3 都是有序的,但是不能由此保证整体有序。 而第二段序列,局部 2 3 4,4 5 6,6 8 10 都是有序的,而且相邻局部都有一个重合元素, 所以保证了序列整体也是有序的。
[2 3 4 1 2 3]
[2 3 4 5 6 8 10]
基于这种思想,我就构思三种非递归遍历的统一思想:不管是先序,中序,后序, 只要我能保证对每个结点而言,该结点,其左子结点,其右子结点都满足以先序/中序/后序的访问顺序, 整个二叉树的这种三结点局部有序一定能保证整体以先序/中序/后序访问,因为相邻的局部 必有重合的结点,即一个局部的“根”结点是另外一个局部的“子”结点。
如下图,对二叉树而言,将每个框内结点集都看做一个局部,那么局部有 A,A B C,B D E,D,E,C F,F,
A
/ \
B C
/ \ \
D E F
并且可以发现每个结点元素都是相邻的两个局部的重合结点。发觉这个是非常关键的,
因为知道了重合结点,就可以对一个局部排好序后,通过取出一个重合结点过渡到与之相邻的
局部进行新的局部排序。我们可以用栈来保证局部的顺序(排在顺序前面的后入栈,
排在后面的先入栈,保证这个局部元素出栈的顺序一定正确),然后通过栈顶元素(重合元素)
过渡到对新局部的排序,对新局部的排序会导致该重合结点再次入栈,
所以当栈顶出现已完成过渡使命的结点时,就可以彻底出栈输出了(而这个输出可以
保证该结点在它过渡的那个局部一定就是排在最前面的),而新栈顶元素将会继续完成新局部的过渡。
当所有结点都完成了过渡使命时,就全部出栈了,这时我敢保证所有局部元素都是有序出栈,
而相邻局部必有重合元素则保证了整体的输出一定是有序的。这种思想的好处是将算法与顺序分离,
定义何种顺序并不影响算法,算法只做这么一件事:将栈顶元素取出,使以此元素为“根”结点
的局部有序入栈,但若此前已通过该结点将其局部入栈,则直接出栈输出即可。
从实现的程序中可以看到:三种非递归遍历唯一不同的就是局部入栈的三行代码的先后顺序。 所以不管是 根->左->右,左->根->右,左->右->根,甚至是 根->右->左,右->根->左,右->左->根 定义的新顺序,算法实现都无变化,除了改变局部入栈顺序。
值得一提的是,对于先序遍历,大家可能发现取出一个栈顶元素,使其局部先序入栈后, 栈顶元素依然是此元素,接着就要出栈输出了,所以使其随局部入栈是没有必要的, 其代码就可以简化为下面的形式。
void preorderTraversalNew(TreeNode *root, vector<int> &path)
{
stack<TreeNode *> s;
s.push(root);
while(!s.empty())
{
root = s.top();
s.pop();
if(root == NULL)
{
continue;
}
else
{
path.push_back(root->val);
s.push(root->right);
s.push(root->left);
}
}
}
最后我再说两句
为了标记第几次进栈,作者统一地给所有的结点 attach 了一个额外的属性,带来了空间开销
上面使用的 make_pair 在 Java 中对应的就是 Pair 泛型类, 它在 javafx.util 包中,类构造函数有两个参数,键及对应值:
public class Pair<K,V>
Pair<Integer, String> pair = new Pair<>(1, “One”); // 使用示例
Integer key = pair.getKey();
String value = pair.getValue();
很适合给 TreeNode 做 attachment
转载部分来自:紫松
出处:简书中的博客
2020 年 08 月 08 日更新
今天才知道原来遍历二叉树还有其他方法,比如 Morris 中序遍历法。
Morris 中序遍历法
前面的迭代法遍历需要 O(n) 空间的栈,递归法遍历则需要函数栈空间,但是 Morris Traversal 只 需要 O(1) 的空间复杂度。
这么神奇的吗?我们来看看具体做法(算法文字描述来自 LeetCode 解答):
假设当前遍历到的结点为 xx):
如果 xx 无左孩子,则访问 xx 的右孩子,即 x = x.\textit{right}x=x.right。
如果 xx 有左孩子,则找到 xx 左子树上最右的结点(即左子树中序遍历的最后一个结点,xx 在中序遍历中的前驱结点), 我们记为 predecessor。根据 predecessor 的右孩子是否为空,进行如下操作:
a. 如果 predecessor 的右孩子为空,则将其右孩子指向 xx,然后访问 xx 的左孩子,即 x = x.left;
b. 如果 predecessor 的右孩子不为空,则此时其右孩子指向 xx,说明我们已经遍历完 xx 的左子树,我们 将 predecessor 的右孩子置空,然后访问 xx 的右孩子,即 x = x.right。
重复上述操作,直至访问完整棵树。
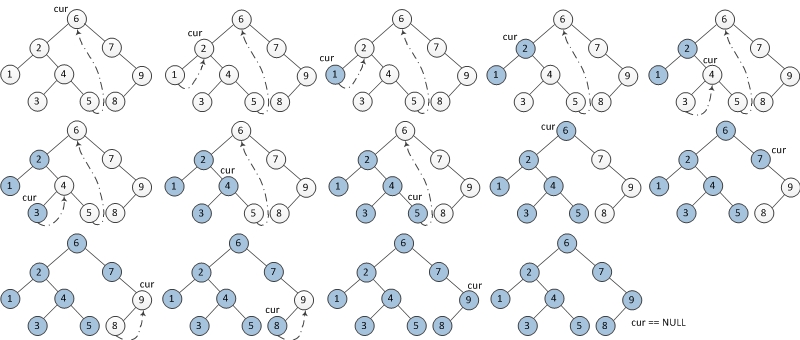
可以看到,关键在于遍历过程中修改了树结构,产生了环以便于孩子结点遍历完后再返回父结点,通过查看 前驱结点右孩子是不是指向自己来确定是不是第二次到达当前结点(中序遍历第二次到达结点时进行访问)。
代码实现如下:
class Solution { // Morris 中序遍历
public void morrisTraversal(TreeNode root) {
TreeNode cur = root;
while (cur != null) {
// 没有左孩子
if (cur.left == null) {
process(cur);
cur = cur.right; // 向右走
continue;
}
// 有左孩子
var pred = predecessor(cur); // 后继子
if (pred.right == cur) { // 说明这是第二次到达此结点,左孩子已经被访问过了
pred.right = null; // 去掉环,保证树结构完好如初
process(cur);
cur = cur.right;
} else { // pred.right==null,说明这是第一次到达此结点
// 不访问此结点,直接左转
pred.right = cur; // 添加回环
cur = cur.left;
}
}
}
private TreeNode predecessor(final TreeNode cur) {
var node = cur.left;
while (node.right != null && node.right != cur) { // 注意需要 node.right != cur 防止死循环
node = node.right;
}
return node;
}
private void process(TreeNode cur) {
// 树调试技巧:先依次打印遍历的结点,确定遍历顺序无误后再尝试打印各个结点的状态
// System.out.println("" + cur + "(" + cur.val + ") " + cur.left + " " + cur.right);
// 具体对结点的访问操作
// ......
}
}
最后附上GitHub:https://github.com/gonearewe